Optimal transport for cross-ligual document retrieval

In this post I would like to detail the ideas behind our ECIR 2018 paper, titled Cross-lingual Document Retrieval using Regularized Wasserstein Distance. In case the paper’s title sounds complicated, bear with me as the central idea is straight-forward. The paper builds on the seminal work of M. Kusner et al. where they propose to combine the expressiveness of word embeddings with the theory of optimal transport.

The problem of optimal transport

The problem of optimal transport is a well-studied problem with a long history and lot’s of work from famous mathematicians (Monge, Kantorovich, Vilani, …). In its original formulation by Monge the problem is defined as follows:

Given two distributions of equal masses, find a transport map $\gamma$ which transfers the first distribution to the second and minimizes the associated transport cost.

There are mathematical formulations for the problem both for the continuous and the discrete case. For simplicity, I will skip them in this post as they can be found both in the paper and in several textbooks: e.g., from G. Peyré and M. Cuturi here and from L. Ambrosio here.

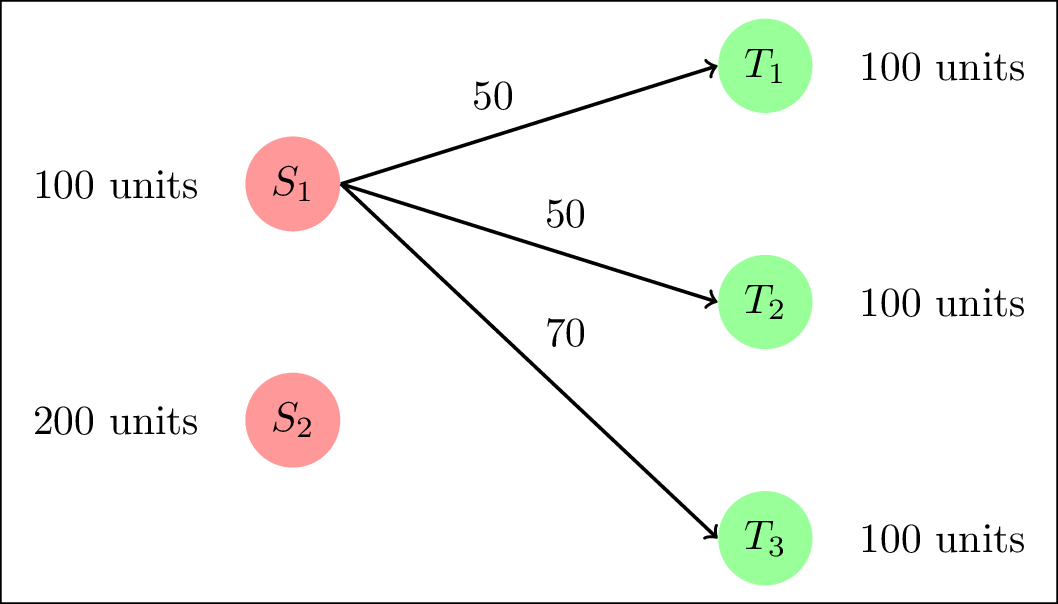
To make the problem formulation more clear, let’s graphically illustrate it using a bipartite graph as an example. Imagine the problem of having two factories preparing croissants denoted as factory $S_1$ and $S_2$ and, three bakeries that sell these croissants: $T_1$, $T_2$ and $T_3$. Transfeting croissants from the source factories $S_i$ to the target bakeries $T_j$ involves different costs depending for instance on their distance. The optimal transport problem seeks the solution of transfering all the croissants from the factories $S_i$ to the bakeries $T_j$ while minimizing the associated cost of transfer. In the following figure for instance, I illustrate the source and the target points, the availability and the demand for croissants, and the costs from $S_1$ to $T_j$. There are similar costs for $S_2$ but not shown in the figure to keep it readable. Notice how the availability (200+100) equals the demand (3$\times$100) for croissants.

A more general case is shown in the figure below, where all the partial costs between the sources and target nodes are shown and their values are the elements of the array $D$. An associated array $\gamma$ is shown: this is the transport plan that describes the mass that will be transported from the source nodes to the target nodes. For example, the $\gamma_{i,j}$ element is the amount of mass (croissants) that will be transfered from $S_i$ to $T_j$. The total cost of the transportation is the sum of the element-wise multiplication between $D$ and $\gamma$.

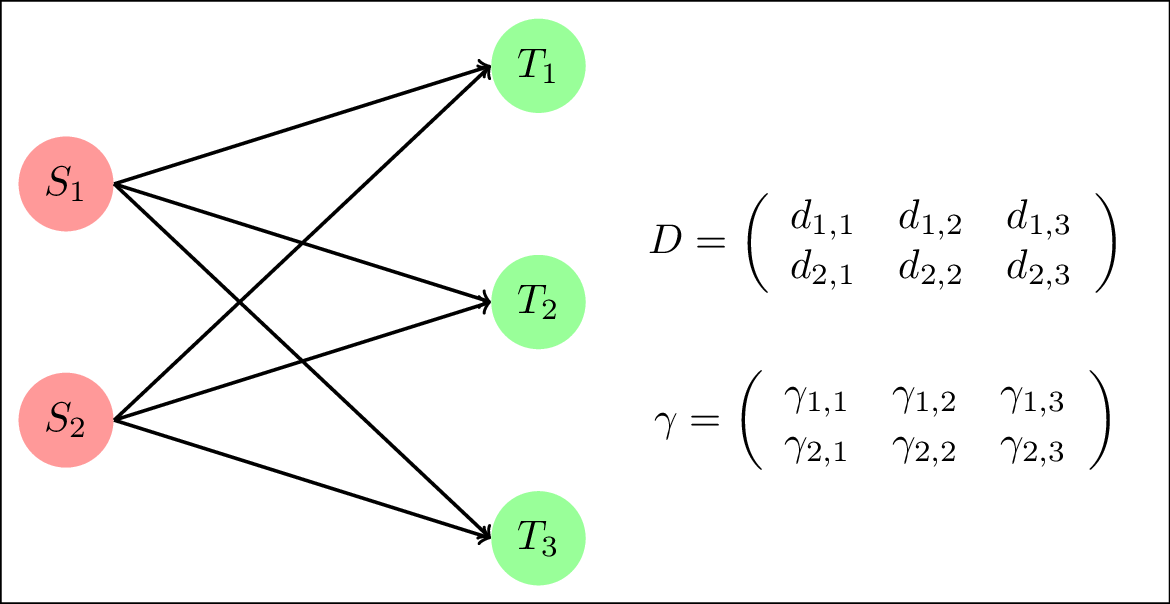
Summarizing, the optimal transport problem tries to minimize the cost of transfering one distribution to another. The distance between these two distributions is called Wasserstein distance and it is also known as Earth Movers distance. Mathematically, given two distributions $\mu_S, \mu_T$ the Wasserstein distance between them is the solution to the minimization problem $W(\mu_S, \mu_T)= \min_{\gamma \in \Pi(\mu_S, \mu_T)}\langle A, \gamma\rangle_F$, where $\Pi$ is the set of possible transport plans between the two distributions while $\langle\cdot, \cdot \rangle$ is the Frobenious dot product between matrices (fancy name for the generalization of the inner product for matrices).

Optimal transport and text

The nice idea of M. Kusner et al. is to combine the discrete distributions (bag-of-words) of documents and the expressiveness of word embeddings. Instead of croissant factories and bakeries in the sides of the above bipartite graphs we have bag-of-words document representations. And to estimate the costs of transfering the words of the documents between them, we use word embeddings. Again, the figure below taken from the paper of Kusner et al. illustrates this idea.

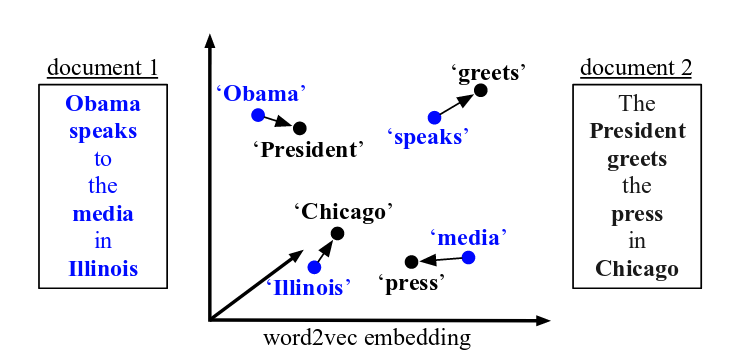
Notice that while the input documents 1 and 2 do not share any common words (apart from stop-words) they are semantically very similar. The reason why they are semantically similar is shown in the middle of the figure that shows the per-word similarities captured by the word embeddings. That said, the distance of the two documents can be calculated by solving the optimal transport problem:

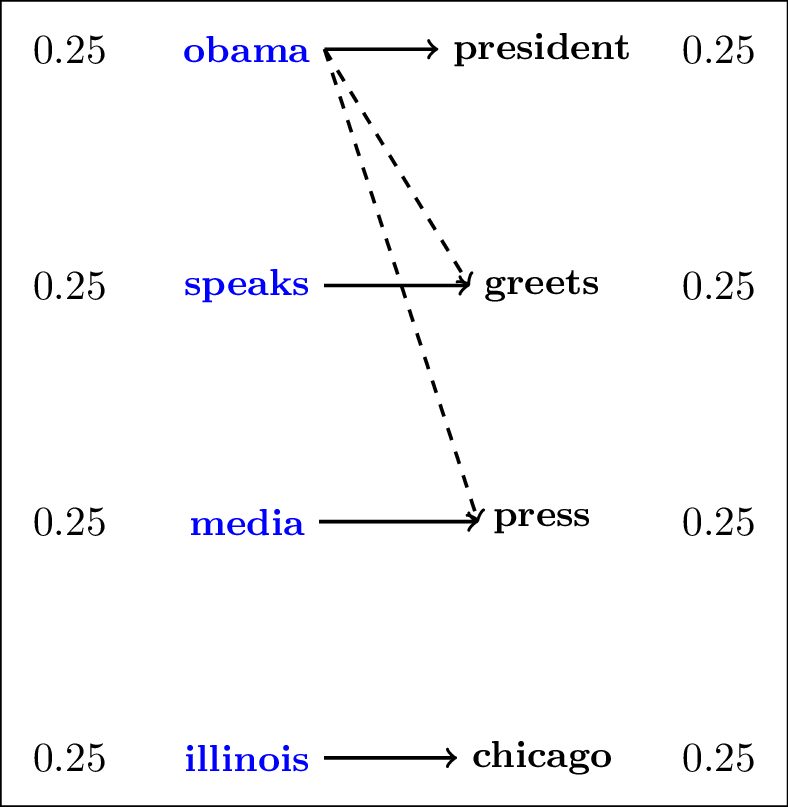
In this graph, documents 1 and 2 are sparse bag-of-words distributions $l_1$-normalized term frequency co-efficients. The normalization ensures that the source and the target distributions are of equal size. Naturally, the distances between the graph elements can be calculated by taking the Euclidean distance between the embeddings of the words. This distance metric is called Word Movers Distance (similar to Earth Movers Distance), and works quite well in practice. Two of the limitations of this distance measure are:

1. the computational complexity as for each document pair an optimization problem needs be solved, and
2. the smoothness of the transport plan as it turns out that the minimization problem results in a dense matrix $\gamma$.

Adding regularization to the Wasserstein distance

M. Cuturi recently proposed to add regularization to the Wasserstein problem. Instead of solving

\[W(\mu_S,\mu_T) = \min_{\gamma \in \Pi(\mu_S, \mu_T)}\langle A, \gamma\rangle_F\]

he suggested to solve

\[W(\mu_S, \mu_T)= \min_{\gamma \in \Pi(\mu_S, \mu_T)}\langle A, \gamma\rangle_F - \frac{1}{\lambda}E(\gamma)\]

where $E(\gamma)$ is the entropy of the transport plan and $\lambda$ is a parameter to be tuned that controls the effect of the regularization term. Two very important advantages stem from the addition of the regularization term which are of interest for the text applications we are interested in:

1. The optimization problem can be solved by an iterative algorithm called Sinkhorm Knopp, which has linear complexity $O(n)$. Compared to the cubic complexity when not using regularization this is a nice boost. Also, Sinkhorm Knopp involves matrix multiplication that can be accelerated by the use of GPUs.
2. Regularization results in a smoother transport plan, with less conncetions. I will illustrate these points in a following example.

Cross-lingual document retrieval

Known search cross-lingual retrieval is the task where given a query, one must retrieve one document from a set of documents that responds to the information need as described by the query. In the known search problem, we know in advance that there is a single document that satisfies the information need. One realistic scenario for the problem is Wikipedia. Wikipedia documents are written in different languages; documents that discuss the same topic are linked with inter-language links. It is common to take advantage of these links to construct interesting cross-lingual tasks and cross-lingual retrieval is one of them. A query document is given in language $l_1$ (English for example) and the associated document written in another language (French for example) must be retrieved. The documents between languages may be exact translations, broad translations in the sense that parts of a source document (usually of the English) have been translated in another language or just semantically associated as they were written from different people for the same subject.

Applying the Wasserstein distance for cross-ligual retrieval in this case relies on estimating the distance of the query documents with the documents to be retrieved and proposing the document with the smallest distance.

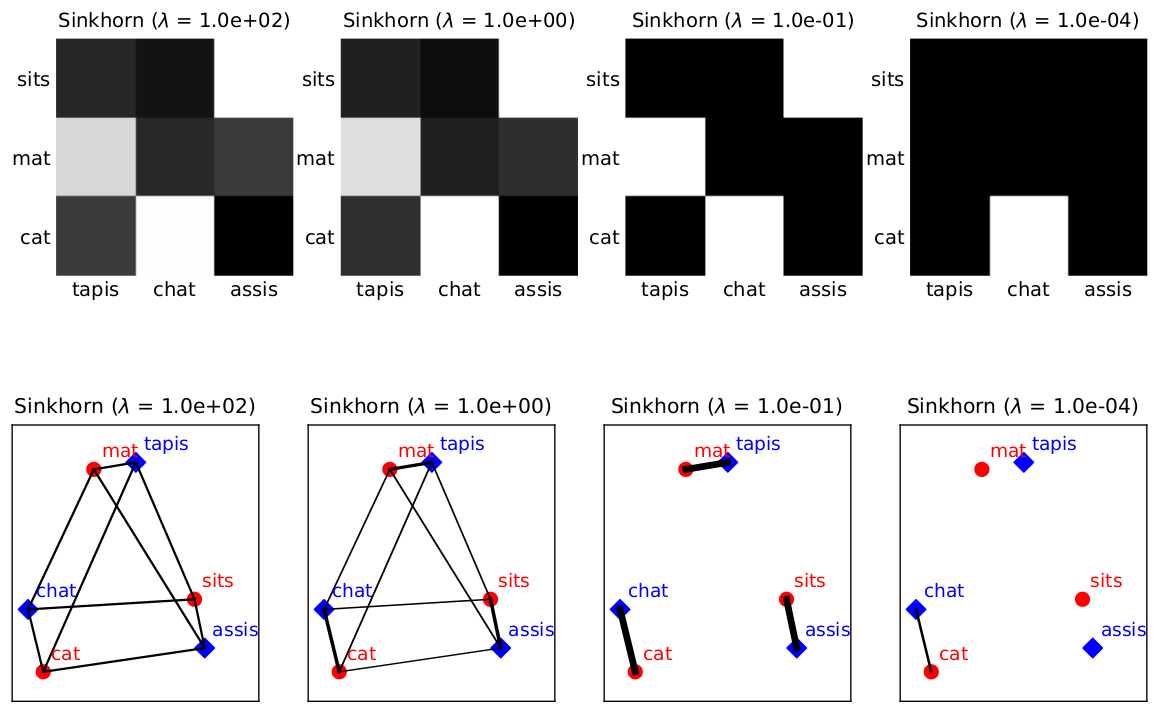
The effect of regularization

In the figure below I illustrate the effect of the regularization when solving the minimization problem. There are two sentences whose distance we want to calculate: “The cat sit on the mat” and its translation in French “Le chat est assis sur le tapis”. The figure show the transport plan between the words of the sentences for different values of $\lambda$, which is the regulatization coefficient. Notice that the optimal associations are obtained for $\lambda=0.01$ while for other values the transport plan is suboptimal.

Results

It turns out that high quality cross-lingual word embeddings with the Wasserstein distance perform really well. In particular, they outperform the neural bag-of-words baseline by a large margin as well as topic models and a method that relies on translation. Further, the regularized version of the Wasserstein distance performs better than the simple version, which is interesting! For more information and details on the experimental part, take a look at the paper results!